
垂心拋物線
遙想當年高三的時候太無聊
就隨便畫隨便證明
意外的發現了這個現象:
如果有一線段AB、平行於一直線L
有一個點 P
沿著直線L移動
則△ABP的垂心軌跡
將會形成一條拋物線!
(垂心:三角形的三個高交會的那個點)


那要怎麼證明呢?
當然還是得先訂個座標
直接把L當作x軸
然後AB正中間作中垂線當作y軸
讓A點座標是(-a,b)
讓B點座標是(a,b)
讓P點座標是(p,0)


再來就是要找到垂心H的座標了!
垂心的特性
因為是三角形三邊的「高」
所以要掌握的就是垂直的特性
然後因為高一定是從頂點出來
我們就知道H的x座標
一定是跟著P點在走
也就是說H的座標可改成 (p,y)

那再來比較麻煩的就是H的y座標了
要注意的是
這邊我們希望要找的是y跟p之間的關係
先放大一點來看
BD、PC分別是兩條高
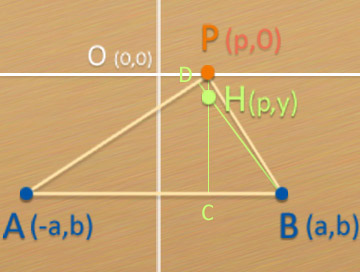
PC一定垂直於AB這不用管它
重點在於BD垂直於AP
也就是說BH也垂直於AP
所以現在要計算的就是讓BH向量、可以垂直於AP向量
BH向量為 (p-a, y-b)
AP向量為 (p+a, -b)
向量若為垂直
則內積為0
向量BH‧AP
= (p-a)*(p+a) + (y-b)*(-b)
= p2 - a2 - by + b2
= 0
所以
by = p2 - a2 + b2
y = (1/b) p2 + (b2 - a2)/b
由此可知y和p的關係正好是拋物線!
且由於b<0,所以這是一個開口向下的拋物線
(不過要注意的是這邊的直線L並不是準線喔)
總之大家有空可以畫畫看囉!

全站熱搜


 留言列表
留言列表
